Que ce soit dans Minecraft ou au fin fond d’une vallée du Nouveau Mexique, le processus de minage désigne le fait d’extraire un minerai (précieux, de préférence). Ce processus est généralement pénible et demande un investissement et une prospection préalables de l’environnement et du marché.
Blockchain
La blockchain est un registre composé de petits blocs reliés entre eux. Chaque bloc contient une liste de transactions, et est relié au bloc précédent par un processus cryptographique.
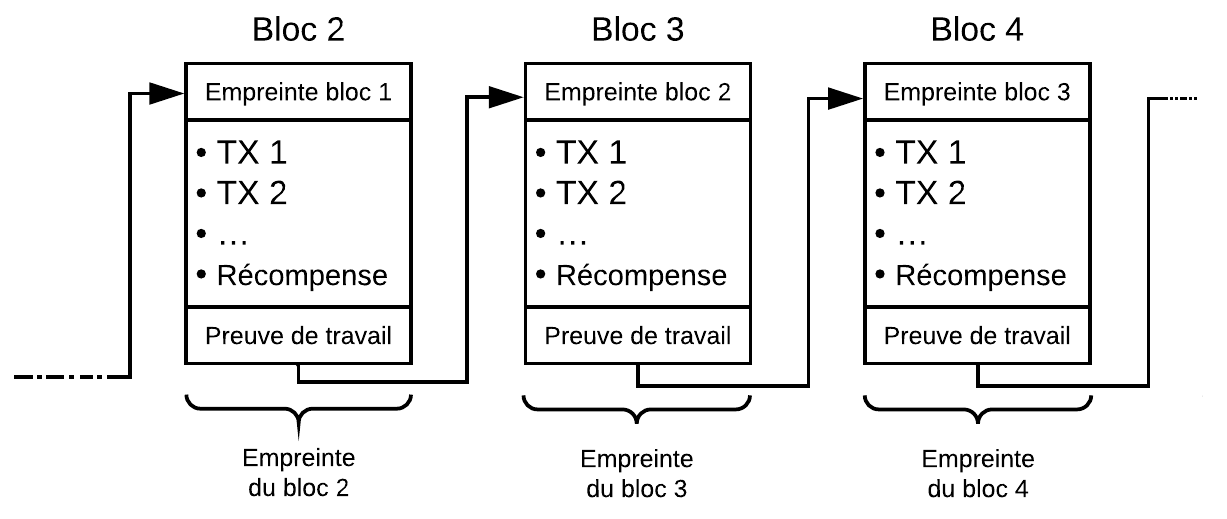
Ce système repose sur 3 principes :
- Un bloc ne peut être généré que lors qu'un certain temps ait passé après le bloc précédent ;
- Le réseau – dans son ensemble – a majoritairement une bonne intention ;
- Chaque bloc contient l’empreinte du précédent.
Hash (empreinte)
Une empreinte (ou hash) est une valeur obtenue après avoir appliqué une somme de contrôle (un calcul mathématique appelé fonction de hashage) à une donnée de départ. Cette fonction de hashage est telle qu'un changement infime de la donnée de départ produit une empreinte totalement différente de la première.
Exemple :
Si le mot « salut » produit l’empreinte 94 856,
le mot « qalut » qui n’a changé que d’une lettre, produit l’empreinte 26 590, radicalement différente de la première.
De par la nature de cette fonction de hashage, il est impossible de deviner l’origine d’un hash : Toute la cryptographie actuelle repose sur cette incapacité à reproduire la donnée de départ à partir d’une empreinte.
Ceci dit, revenons au 3e principe de la blockchain, qui protège l’immutabilité de cette dernière : La modification d’un élément à l’intérieur d’un bloc quelconque changerait son empreinte de façon considérable. Du fait que le bloc suivant doive référencer cette empreinte, il faudrait donc le modifier, lui aussi, pour camoufler l’attaque ; sinon, l’ensemble du réseau se rendrait compte que le bloc falsifié est faux et le rejetterait.
Mais si l’assaillant décide effectivement de modifier le bloc suivant, il devrait continuer jusqu'à modifier tous les blocs. C’est là qu'il se heurte aux 1er et 2e principes.
Vu que l’assaillant possède moins de force que le reste du réseau, il générera toujours moins de blocs que les autres et sa chaîne serait moins longue. De là, il est alors simple de décider quelle chaîne a « raison » : La chaîne la plus longue.
Le premier principe s’assure ici que l’assaillant prendrait du temps pour générer un nouveau bloc, et le 2e principe s’assure que le reste du réseau sera plus rapide que lui.
La difficulté
Pour qu'un bloc ne soit généré qu'après un certain temps, on demande au nœud une preuve de travail : c’est-à-dire un élément qui démontrerait qu'il a fourni un effort pendant une certaine durée.
Ce qui est demandé : un hash dont la valeur dépasse un certain seuil. Nous associons donc à chaque hash sa valeur numérique ; le hash de « salut » (94 856) serait dans ce cas supérieur au hash de « bonjour » (34 117) (94 856 > 34 117).
Imaginons donc que nous définissions un seuil de 50 000. Comment trouver un hash dont la valeur est égale ou dépasse ce seuil ?
Certes, un seul hash égal à 51 000 suffirait. Mais du fait qu'on n’ait aucun moyen de trouver quelle donnée possède l’empreinte 51 000, la seule façon de procéder serait d’essayer plusieurs éléments, de calculer leur empreinte à chaque fois et de comparer avec notre seuil.
Dans notre exemple, le nombre d’empreintes possibles est de 100 000 (soit des valeurs allant de 0 à 99 999). À chaque fois que nous prenons une donnée et calculons son hash, nous trouvons une valeur différente, mais toujours dans cet intervalle. Il y a donc 50 000 données qui ne conviennent pas et 50 000 qui conviennent. En prenant un élément au hasard, comme « hello », nous avons une chance sur deux que son empreinte soit valide comme preuve de travail. Dans un cas sur deux, elle ne conviendrait pas et nous devrions fournir un travail supplémentaire pour trouver une « solution ».
Ce processus (basé sur le hasard et une fonction cryptographique) nécessite « du temps » de traitement et de l’énergie. Nous comprenons donc ici que ce système de preuve de travail remplit son rôle, vu qu'il nous fait travailler.
Exemple :
Si nous considérons un seuil de 75 000, un quart des éléments pris au hasard conviendrait et trois quarts ne conviendraient pas. Si nous avons besoin de 10 secondes pour décider d’un mot au hasard et calculer son empreinte, on est supposé perdre 30 secondes à générer des empreintes qui ne serviraient à rien. Bien sûr, nous pouvons avoir un coup de chance et en générer une qui serait utile dès la première tentative, mais ces coups de chance n’arrivant pas de façon répétée, nous pouvons être sûrs qu'en moyenne, on générerait une empreinte correcte toutes les 30 secondes (ajoutées à cela 10 secondes pour créer l’empreinte utile).
Imaginons maintenant que nous n’ayons le droit de construire un bloc que si nous créions une preuve de travail dont l’empreinte dépasse 90 000. Pour 9 éléments pris au hasard et dont nous aurions calculé le hash (9 fois 10 secondes), nous trouverions 1 élément qui nous permettrait de créer un bloc. Étant le seul acteur de notre réseau, nous remarquerions que la moyenne de temps entre un bloc et un autre est de 100 secondes.
Ce seuil dont nous parlons est communément appelé « difficulté ».
Avec plusieurs acteurs, il serait donc important d’ajuster (augmenter et réduire) cette difficulté pour que le temps de génération du bloc reste toujours le même.
Les transactions et l’UTXO
Lorsqu’une personne veut envoyer de l’argent à une autre, elle crée une transaction. La transaction est une instruction : « la personne A transfère la valeur X à la personne B ».
Mais ce n’est pas tout ; la personne A, pour rassembler la somme à envoyer, va d’abord piocher dans ses reçus. En faisant cela, elle crée ce que nous appelons une « entrée » ; donc une liste d’anciennes transactions dont elle n’a pas encore dépensé la valeur.
Ensuite, la personne A définit une liste d’adresses parmi lesquelles partager la valeur rassemblée ; généralement, elle offre la valeur X qu'elle voulait envoyer à la personne B et renvoie le reste (la monnaie) à une de ses adresses.
Ce système est appelé « UTXO », pour « unspent transaction output ».
De cette manière, il est possible de remonter l’origine d’une pièce jusqu'au bloc où elle a été générée, et de cette façon, en vérifier l’authenticité. On évite aussi de dépenser une pièce plusieurs fois ou de dépenser des pièces qu'on n’a pas reçues.
La vérification des transactions
Vu que le système demande une preuve de travail pour qu'un acteur puisse créer un bloc et l’ajouter à l’ensemble (la Blockchain), il y a des transactions qui sont créées pendant le temps qu'il faut pour fournir cette preuve de travail.
Lorsqu'une personne crée une transaction, elle la diffuse à des nœuds du réseau. Un nœud va donc écouter et réceptionner les transactions ainsi créées.
Pour chaque transaction, il va remonter l’origine des pièces et s’assurer que chacune est authentique et bien en possession du destinateur. Grâce à l'UTXO, donc, il n’est pas nécessaire de connaître ou d’enregistrer le « solde » d’un compte.
En cas de souci, la transaction est rejetée. Si tout est en ordre, le nœud la garde en attente. L’ensemble des transactions en attente est appelé un « mempool » (memory pool).
Le block
Après avoir créé une preuve de travail (et donc fourni un effort), le nœud pioche dans la file d’attente des transactions (qu'il aura vérifiées) pour les inclure dans son bloc nouvellement créé. Comme récompense à son travail, le nœud a le droit d’inclure une transaction spéciale : une instruction qui lui attribue une certaine quantité de pièces de monnaie à lui-même.
Il assemble donc un certain nombre de transactions, ajoute à cela la preuve de travail créée, sa récompense, l’empreinte du bloc précédent et enregistre le tout dans une base de données. Du fait qu'elle soit composée de blocs reliés entre eux, cette base de donnée est appelée « blockchain ».
Le bloc nouvellement créé est diffusé sur le réseau pour que tous les autres nœuds l’inscrivent dans leur exemplaire de la base de données. Ils vérifient bien sûr le contenu et que l’empreinte du bloc précédent, inscrite dans ce nouveau bloc, convient et que la preuve de travail est correcte.
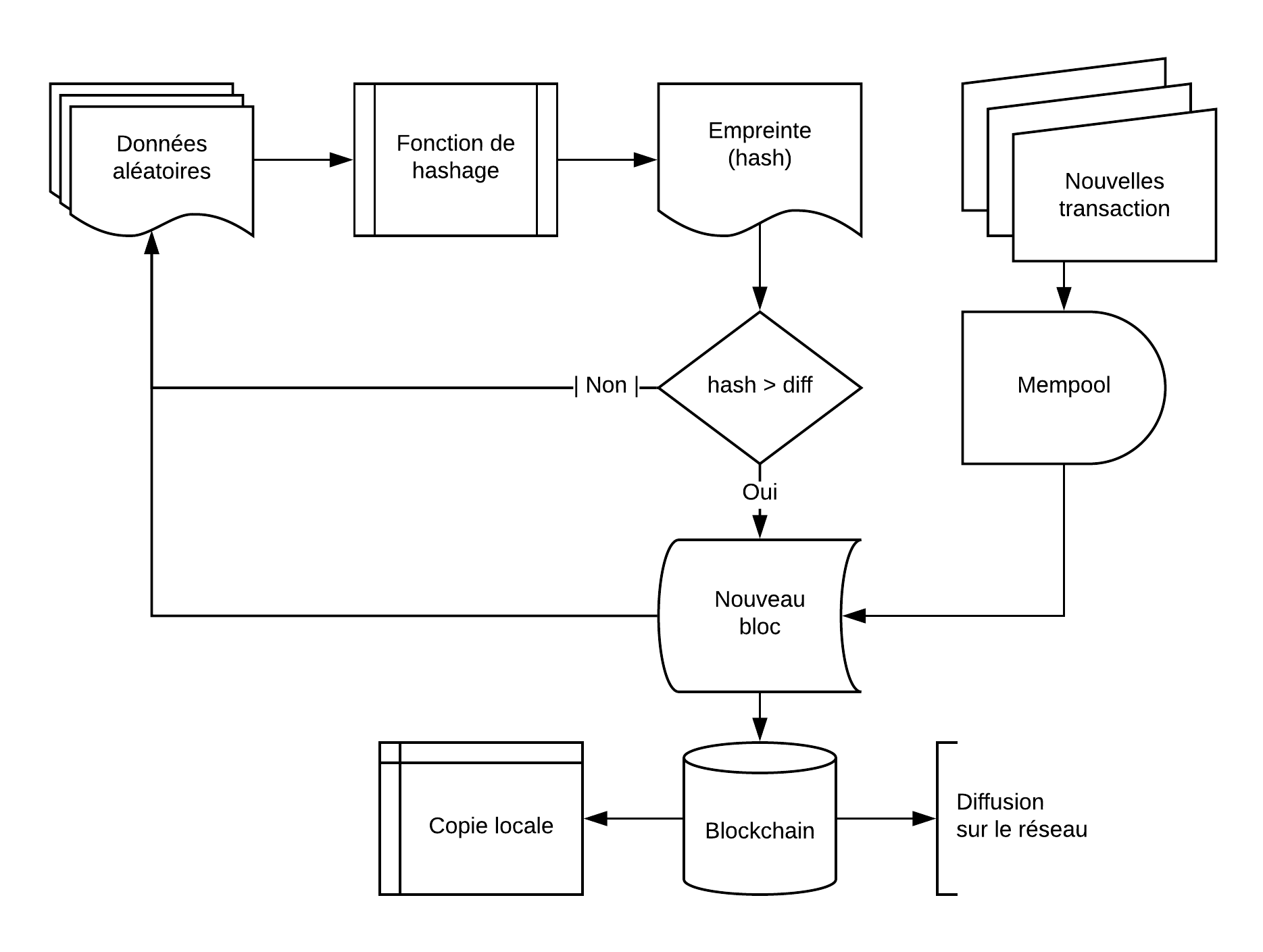
Le consensus
Un nœud malintentionné pourrait vouloir créer de fausses transactions. Mais de par la nature de ces transactions, les autres nœuds refuseraient d’inclure son bloc et il devrait créer lui-même le bloc suivant, ainsi que le bloc d’après et jusqu'à ce que les autres reconnaissent sa chaîne comme chaîne principale.
Mais grâce au système de difficulté et du fait qu'il y ait plusieurs nœuds sur le réseau, le nombre de blocs créés par un nœud est proportionnel à sa vitesse de calcul : c’est-à-dire la vitesse à laquelle il peut générer des hash pour dépasser la difficulté (ce qui lui permettrait de générer un bloc).
Exemple :
S’il existe 5 nœuds sur le réseau et que chacune nœuds peut prendre 10 mots aléatoires et calculer leur hash toutes les minutes, alors le réseau en entier essaierait 50 hash par minute.
S’il faut essayer en moyenne 100 hash pour dépasser la difficulté, alors un bloc serait généré sur le réseau toutes les 2 minutes (deux fois 50).
Un seul nœud, dans ce cas, même très chanceux, ne pourrait jamais générer à lui seul tous les blocs du réseau ; sa vitesse de 10 hash / minute ne lui permettrait de créer un bloc que toutes les 10 minutes ; et le temps qu'il en crée un, le reste du réseau en aurait déjà créé 4. La chaîne de l’assaillant serait donc moins longue que la chaîne des autres nœuds ; de 4 blocs. Et 10 minutes plus tard, alors qu'il aura créé un deuxième bloc, la chaîne serait plus longue que la sienne de 8 blocs. Lorsqu'un nouveau nœud rejoint le réseau, et s’il a besoin de savoir à quelle blockchain faire confiance, il lui suffirait de prendre la chaîne la plus longue.
Ce système repose, bien évidemment, sur l’idée que la majorité du réseau est bienveillante. Nous parlons dans ce cas de « consensus ». Si ce n’est pas le cas, il ne sert à rien d’utiliser le réseau (l’écosystème serait trop instable pour être viable).
Le minage
Le système de « vote » dont nous venons de parler repose la vitesse à laquelle un nœud essaie des hash. La technologie étant différente d’un nœud à l’autre, certains ont tendance à avoir plus de poids que les autres (un nœud qui essaierait 20 mots par minute pourrait générer deux fois plus de blocs qu'un nœud qui essaie 10 mots par minute).
Afin d’éviter ce déséquilibre des forces, il est possible que le nœud minoritaire améliore son matériel, pour augmenter sa vitesse. Ceci a pour effet de rééquilibrer le réseau et d’éviter qu'un acteur unique soit majoritaire et ait le pouvoir de falsifier les transactions. Mais là n’est pas le seul avantage ; en doublant sa puissance de calcul, un nœud doublerait aussi sa récompense, vu qu'il doublerait le nombre de blocs générés.
Cette compétition devient encore plus intéressante lorsque l’on considère que la valeur des pièces obtenues augmente avec l’augmentation du nombre de compétiteurs ; en effet, du fait que le temps de bloc reste le même, le nombre de pièces obtenues par un nœud sur un réseau de 5 nœud ne serait pas le même que la récompense obtenue par un nœud sur un réseau qui en compte 10.
Cette ruée vers l’or contribue donc à la rareté de la monnaie, et à l’augmentation de sa valeur.
Les pools
Lorsque l’on contribue à hauteur de 1 / 1000 de la puissance du réseau, on peut s’attendre à trouver un hash dépassant la difficulté 1 fois tous les mille blocs. En restant sur le même exemple, rappelons que la difficulté fait que chaque génération de bloc nécessite 10 minutes au réseau entier. On s’attendrait donc à pouvoir générer un bloc, seul, tous les 6 jours. Mais plus le réseau s’élargit, moins on en génère seul, et il peut arriver qu'on passe des mois entiers sans pouvoir générer aucun bloc ; sans aucune garantie de le faire et sans garantie de pouvoir garder la machine fonctionnelle aussi longtemps.
Lorsqu'il n’est plus suffisant de « miner » seul pour créer un bloc, il est possible que plusieurs personnes s’allient à un même nœud pour le faire profiter de leur puissance de calcul et augmenter son poids sur le réseau. Ces « coopératives » minières sont appelées « pools ».
La récompense de chaque bloc créé par le nœud est distribuée à tous les « mineurs » du pool, proportionnellement à leur contribution (soit le nombre de hash qu'ils ont généré pour le bloc en question). Certains pools offrent aussi une récompense supplémentaire au mineur qui avait généré le hash dépassant la difficulté du réseau.
De cette façon, les mineurs sont toujours récompensés pour le temps passé à fournir des preuves de travail au réseau et l’équilibre des forces est garanti.
Le mineur
Un mineur est donc un matériel informatique capable de générer des « mots » aléatoires et d’exécuter des fonctions cryptographiques pour en dériver les « hash ». Ces hash sont soumis à un pool qui les compte et vérifie si l’un d’eux dépasse la difficulté du réseau. Lorsqu'un nouveau bloc est généré, le pool partage équitablement la récompense avec les mineurs.
De par la nature de la fonction cryptographique, certains matériels peuvent générer plus de hash par seconde que d'autres ; d’où l’unité de calcul de vitesse de minage : le hash par seconde : H/s.
Ses multiples sont :
- Le kilo-hash/s (kH/s) : 1000 h/s
- Le méga-hash par seconde (MH/s) : 1 million h/s
- Le téra-hash par seconde (TH/s) : 1 milliard h/s
- Le péta-hash par seconde (PH/s): 1 billiard h/s
Les fonctions utilisées pour générer ces hash reposent toutes sur le même principe :
Un logiciel (communément appelé « mineur ») prend des éléments aléatoires et les fait passer à travers une fonction cryptographique. La sortie est un hash. Il répète le processus jusqu'à ce que le hash dépasse une certaine difficulté (dictée par le réseau ou le pool). Une fois la difficulté dépassée, les données qui ont servi à produire ce hash sont utilisées (sur le réseau ou soumises au pool). Il répète indéfiniment ce processus.
Par contre, ces fonctions cryptographiques peuvent différer d’une cryptomonnaie à l’autre ; chacune offrant ses propres avantages. C’est ce que nous appelons « algorithme de hashage » (hash algorithm). Certaines fonctions s’exécuteront mieux sur un processeur d’ordinateur, alors que d’autres s’exécutent de manière plus efficace sur un processeur graphique, ou même sur un processeur de téléphone, ou un matériel spécialisé.
Il serait alors plus ou moins rentable, selon la cryptomonnaie que l’on veut miner, de miser sur tel ou tel type de matériel.
Chaque cryptomonnaie possède son propre protocole de preuves de travail (fonction de hash et la façon dont les résultats sont soumis au réseau) et cet algorithme n'est que l’une des facettes qui font de chaque cryptomonnaie un projet unique.
Résumé
Le logiciel de minage répète un processus durant lequel une donnée aléatoire est générée, puis passée par une somme de contrôle pour obtenir un hash. La valeur de ce hash est comparée à une difficulté mise en place par le pool ou le réseau. Si le hash est accepté, il est utilisé comme preuve de travail pour générer un nouveau bloc. Le mineur est récompensé et le nouveau bloc est ajouté à la blockchain, dont chaque nœud possède un exemplaire.
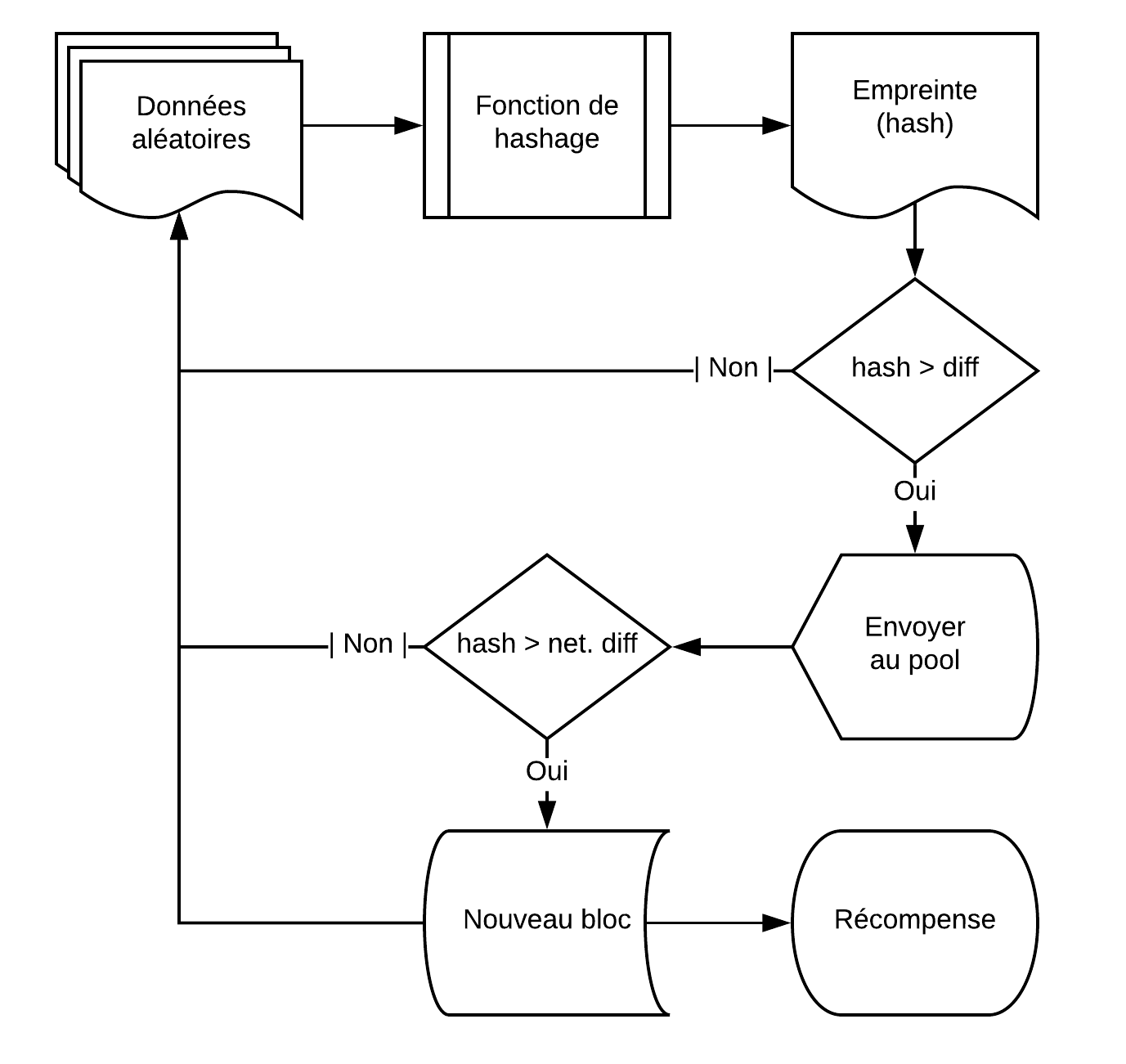
Cette technologie permet la maintenance d'une base de donnée distribuée immutable (que personne ne peut falsifier) et sécurisée (par un consensus), dans laquelle des valeurs peuvent être stockées et échangées de manière sûre.
La Blockchain est l'infrastructure sur laquelle se construit la majorité des cryptomonnaies actuelles ; mais bien qu'elles partagent une technologie semblable, chaque cryptomonnaie possède sa façon de générer de nouvelles pièces et de les distribuer sur son réseau. Toutes sont différentes de par leurs aspirations et leur fonctionnement, mais toutes contribuent à la création d’un système monétaire où aucune entité ne fait loi, ni ne contrôle la génération ou la dépense des pièces de monnaie ou le transfert de valeur ; contribuant ainsi à créer un système fiable, sûr, immutable et décentralisé, un système anarchique mais organisé par des lois mathématiques, où la liberté est réelle.
 Cours écrit par @Jahus.
Cours écrit par @Jahus.
 Si vous avez aimé ce cours, n'hésitez pas à laisser un pourboire :
Si vous avez aimé ce cours, n'hésitez pas à laisser un pourboire :
- ETH / ETC :
0x624688e4012c9E6Be7239BeA0A575F8e41B4B3B6 - BCH / BTC :
1EnQoCTGBgeQfDKqEWzyQLaKWQbP2YR1uU
 Hashtags : #Blockchain, #Minage, #Mining, #Technologie, #Technology, #Block, #Hash, #Pool, #Node, #Noeud, #Bitcoin, #Litecoin, #Dogecoin
Hashtags : #Blockchain, #Minage, #Mining, #Technologie, #Technology, #Block, #Hash, #Pool, #Node, #Noeud, #Bitcoin, #Litecoin, #Dogecoin

